温度って何だろう?
「温度」という概念は、熱力学において中心的な役割を果たします。
と言われてもピンとこないですよね…。
本稿では、「温度」とは一体何なのかを説明していきます。
具体的には、次の3つの項目について順に理解を進めていきましょう。
- 熱的接触
- 熱力学第0法則
- 絶対温度
熱的接触
私たちの体には、「熱い」「冷たい」という、「温度」を感じ取る能力があります。
しかし、感覚は人によって違う上に、測って比べることができません。
そこで、誰もが測定して比較できる、「温度」という概念を定めることが必要となるのです。
では、どうやって決めましょう?
ここで思い出してほしいのが、「熱力学はエネルギーのやりとりを扱う学問である」ということです。
「温度」は、「エネルギーのやりとり」に着目することで決定されます。
例を挙げて考えてみましょう。
高温物体と低温物体を接触させるとどうなるでしょうか?
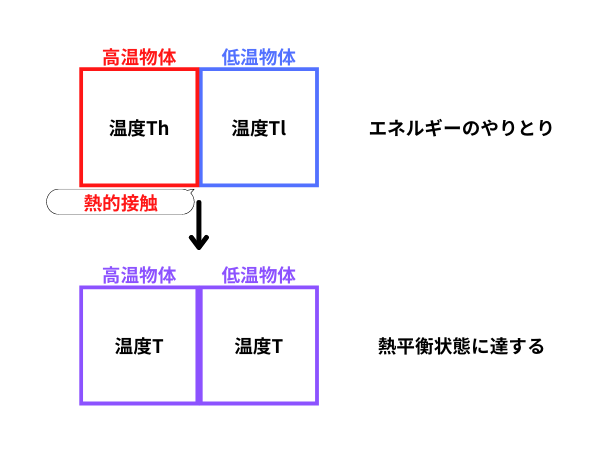
これらの物体の間でエネルギーのやりとりが行われ、高温物体の温度は下がり、低温物体の温度は上がります。
そして、この温度変化は、二つの物体の温度が同じになるまで続きます。この状態は熱平衡状態になっています。
この「互いに等しくなろうとする」性質は、温度の最も重要な性質です。
このように、エネルギーのやりとりを許した接触を、「熱的接触」といいます。
熱力学第0法則
…何やら格好つけた名前の法則が出てきましたね。
熱力学では、第0法則から第3法則までの、全部で4つの法則が出現します。
第1法則以降についても、いずれ出てきますので、楽しみに(?)していてください!
では早速、熱力学第0法則の定義を確認しましょう。
熱力学第0法則の定義
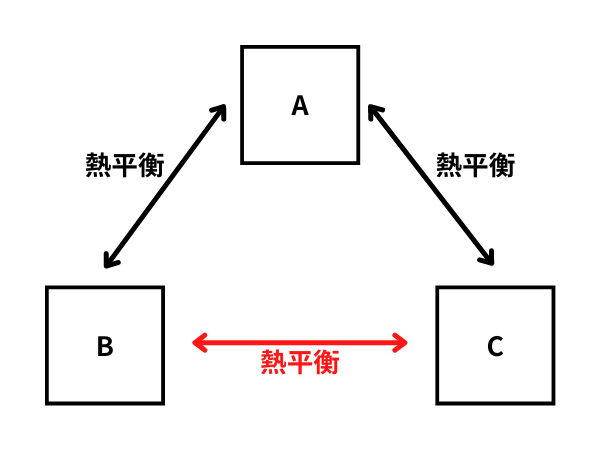
もはや当たり前って感じですね。
第0法則によって、熱平衡状態にある系は同じ「温度」という特性があることを認めています。
この法則を使って温度を知る道具が、皆さんもご存知の「温度計」です。
測りたいものと温度計を熱的接触させて熱平衡状態にして、対象物の温度を知っているのです。
コラム:温度計はなぜ小さいの?
先ほど述べた通り、温度計は、温度計と測定対象を熱的接触させ、熱平衡状態にすることで温度を測定しています。
もし、温度計が測定対象よりも大きかったら、どうなるでしょうか?
熱平衡状態になるとき、測定対象と温度計の温度は、それぞれ同じ温度になるまで変化します。
このとき、温度計が大きすぎると、測定対象の温度が温度計の温度に引きずられて大きく変化し、元の温度が分からなくなってしまいます。
そのため、測定対象の温度が可能な限り変化しないように、温度計は小さく作られているのです。
絶対温度
身近にある温度計には、水銀やアルコールなどが使用されています。
(水銀温度計については、水銀が人体に有毒であることから、最近ではほとんど見なくなりました…。)
同じものの温度をこれらの温度計で測定したとき、どちらも同じ温度を示しますよね。
このように温度を一意的に扱うためには、異なる温度計を使用しても、測定結果がお互いに一致しなくては使いものになりません。
そのためには、何か標準となる温度計を決めて、参照する温度を定義する必要があります。
そこで登場するのが、「絶対温度(理想気体温度)」です。
これは、「理想気体の温度は圧力に比例する」という事実に基づいて決定されています。
ここで、「理想気体」というのは「大きさを持たず、相互作用しない粒子からなる気体」のことです。
(詳細は次回以降の投稿で説明します。)
この温度の単位は「ケルビン(K)」と呼ばれます。
「あれ?温度の単位って『℃』じゃないの?」と思った方、『℃』についてはこの後説明します。
さて、この絶対温度ですが、「温度が圧力に比例する」という関係をそのまま式にすると、次のようになります。
$$T(P) = aP + b$$
ここで、a, bは定数です。このa, bを決めていきましょう。
まずはbです。
理想気体では、圧力がP=0の時、温度はT=0となります。
したがって、b=0です。
次にaです。
こちらは、「水の三重点」から決めていきます。
水の三重点とは、「氷・水・水蒸気が全て共存する固有の温度」のことです。
三重点の温度は、273.16Kと厳密に定義されています。
従って、理想気体温度は、次のようになります。
$$T = 273.16\frac{P}{P_{tp}}$$
ここで、Pは理想気体温度計が示す圧力、Ptpは三重点の圧力です。
ちなみに、先程の273.16Kという値は、当時、氷点と沸点がちょうど100Kになるように決められました。
現在はより正確に測定できるようになり、氷点は273.15K、沸点は373.12Kであることが分かっています。
この理想気体温度ですが、普段の生活では使っていませんよね。
もし使っていたとしたらどうなるでしょうか。
「今日の気温300Kらしいよ。」
「え!あんた312.16Kも熱あるの!?病院いきなさい!」
見たい温度範囲に対して273.16Kがあまりにも邪魔ですね。
私たちが普段の生活で使用するのは、水が氷になったり沸騰したり、せいぜいその程度です。
じゃあ、「氷点273.15Kを引いて、邪魔な部分を消しちゃえ!」ということで生まれたのがこちらです。
$$T_{celsius} = T – 273.15$$
これは、「セルシウス温度」と呼ばれ、温度記号「℃」を使用して表されます。
まさに、私たちが普段使っている温度ですね。
ちなみに、式の通り、理想気体温度とセルシウス温度は、0の位置が違うだけで、温度間隔は全く同じです。
まとめ
今回は「温度」について解説しました。
温度は「熱力学第0法則」と密接に関わっていること、そして「絶対温度」の定義を理解していただければOKです。
次回は、いよいよ「状態方程式」に入っていこうと思います。
数式が増えますが、頑張りましょう!
